Logika Dasar

Logika  adalah  suatu  displin  yang  berhubungan  dengan  metode  berpikir.  Pada  tingkat  dasar,  logika  memberikan  aturan-aturan  dan  teknik-teknik  untuk menentukan  apakah  suatu  argumen  yang  diberikan  adalah  valid.  Berpikir  logis digunakan  dalam matematika  untuk membuktikan  teorema-teorema, dan  dalam  kehidupan sehari-hari  untuk  menyelesaikan  banyak  masalah. Dalam  logika  kita  tertarik  kepada  benar  atau  salahnya  dari  pernyataan-pernyataan (statemen-statemen), dan bagaimana kebenaran/kesalahan dari suatu statemen  dapat  ditentukan  dari  statemen-statemen  lain.  Akan  tetapi,  sebagai pengganti dari statemen-statemen spesifik, kita akan menggunakan simbol-simbol untuk  menyajikan  sebarang  statemen-statemen  sehingga  hasilnya  dapat digunakan dalam banyak kasus yang serupa.

• Proposisi  

Ungkapan sebuah kalimat berita disebut proposisi atau pernyataan. Sebuah proposisi mempunyai ciri bahwa ia benar atau salah atau tidak sekaligus keduanya benar atau salah. Contoh : 3 kurang dari 5 (benar)

• Perangkai     

Dua proposisi dapat dirangkai menjadi satu proposisi oleh ‘dan’, ‘atau’, ‘tidak’, ‘jika, ..., maka’, dah ‘jika dan hanya jika’. Hasilnya disebut suatu proposisi komposit.

Contoh : ‘3²=9’ ; 9 adalah bilangan kuadrat  → ‘3²=9 dan 9 adalah bilangan kuadrat’

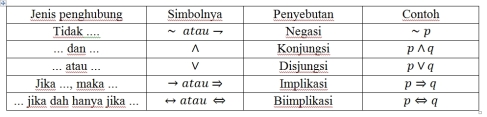
• Notasi

Proposisi dinyatakan dengan huruf-huruf kecil seperi p, q, r, ..., sedangkan peghubung yang merangkai proposisi dinyatakan dengan notasi sebagai berikut:

• Nilai-nilai kebenaran

Nilai-nilai kebenaran suatu proposisi tergantung kepada proposisi-proposisi elementer yang membentuknya.

 Perhatikan table kebenaran berikut:

• Ekivalensi

Dua proposisi disebut ekuivalen jika keduanya sesuai pada setiap baris tabelnya sesuai dalam semua nilai kebenarannya. Jaka kedua proposisi tersebua adalah 𝒜 dan ℬ, jika 𝒜 ekivalen dengan ℬ, maka ditulis 𝒜 ek. ℬ.

• Tautologi, Kontradiksi dan Kontingensi

Sebuah  pernyataan  majemuk  disebut :

1. Tautologi  jika  pernyataan  tersebut selalu  bernilai  benar  untuk  semua  nilai  yang  mungkin  dari  pernyataan-pernyataan komponennya.
2. Kontradiksi  jika pernyataan tersebut selalu  bernilai  salah  untuk  semua  nilai  yang  mungkin  dari  pernyataan-pernyataan komponennya.
3. Kontingensi  (contingency)    adalah  sebuah  pernyataan  majemuk  yang dapat bernilai benar atau salah, bergantung pada nilai-nilai kebenaran dari variabel-variabel pernyataannya.

• Prinsip Dualitas

Dari suatu rumus 𝒜⇔ℬ yang merupakan suatu toutologi dan kedua ruasnya dibentuk semata-matadengan kedua perangkat ‘∧’ dan ‘∨’ dari proposisi-proposisi elementer dan negasinya akan diperoleh suatu rumus lain yang juga suatu toutologi dengan hanya mempertukarkan kedua perangkai tersebut.

• Beberapa Penarikan Kesimpulan yang Sahih :

Beberapa penarikan kesimpulan yang sahih atau valid antaranya adalah modus ponens, modus tolens, dan silogisme.

Perhatikan tabel dbawah ini:

Anda juga bisa download versi PDFnya [Download]